Maths
Fractions

Experiential Education

Objectives

What you will learn:

What a fraction is
Equivalent forms
Simplifying fractions
Performing arithmetic calculations on fractions

Introduction

Many people tend to be wary of fractions but they are simply numbers just like any other number, albeit with certain rules that are applied to make it easier to perform arithmetic operations upon them.

In this series we will explain what a fraction is; explain how to write fractions in different but equivalent forms; look at the techniques for simplifying fractions; and, describe the rule for adding, subtracting, multiplying and dividing with fraction.

What is a fraction?

Let’s start off by looking at just what a fraction is. Fractions are numbers just like any other number. They are typically used to express decimals such as 3.5 or 4.3 and so on.

Fractions are written in a form such as:

\times

{ }

{ blahblah } \times { blah blah }

${ \text{3} \over \text{4} } \text{ or } { \text{15} \over \text{6} }$

The 'professional' format is preferred, however, for this spark module we will largely use the linear format (see below). Otherwise every fraction has to be a screen shot (because it is not within the functionality of the adobe spark pages).

The 'linear' format looks like this:

3/4 or
15/6

In this example, 3/4 the fraction is in a particular mathematical notation whereby the numbers are separating by a bar or ‘vinculum’. It simply means ‘how many times does 4 go into 3?’, or, ‘what is 3 divided by 4?’ This can also be represented by 3 ÷ 4.

Mathematically the top of the fraction is the numerator and the bottom part is the denominator:

${ \text{ Fraction = } } { \text{Numerator} \over \text{Denominator} }$

Types of fractions:

If the denominator is greater than the numerator eg: 4/7 than the fraction is said to be a ‘proper fraction’.

If the denominator is less than the numerator eg: 9/7 then the fraction is said to be an ‘improper fraction’.

Equivalent forms

Fractions may be expressed in different forms but could be the same value (this is what is known as the equivalent form).

For example, we know that 1/2 is 0.5 (one-half) but we also know that 2/4 is one-half as well. Both these fractions are expressed differently but have the same value (one-half). In performing calculations, we tend to express fractions in the ‘simplest form’. The simplest form of 2/4 is 1/2.

The common factor:

An easy way to see if the fraction is in its simplest form is to check if there is a common number (factor) that will go into both the numerator and the denominator.

For 2/4 the common factor for both ‘2’ and ‘4’ is 2 (2 goes into 2 once and into 4 twice). And, this is what it looks like:

${ \text{2 $\div$ 2 } \over \text{4 $\div$ 2 } } { \text { = } } { \text { 1 } \over { 2 } }$

So, to find the simplest fraction, look for those common factors. This will mean some knowledge of the ‘times table’.

For example, express 10/35 in its simplest form.

We know that 5 goes into 10, 2 times, and 5 also goes into 35, 7 times, so the common factor is 5. Therefore;

${ \text{10 $\div$ 5 } \over \text{ 35 $\div$ 5 } } { \text { = } } { \text { 2 } \over { 7 } }$

The highest common factor

Another concept to look at is the ‘highest common factor’. When looking for a common factor to simplify a fraction, we look for the largest (or the highest) common factor which will go into both the numerator and the denominator. Let's look at an example:

Express 12/16 in its simplest form.

We know that 2 goes into both 12:

${ \text{ 12 $\div$ 2 } \over \text{ 16 $\div$ 2 } } { \text { = } } { \text { 6 } \over { 8 } }$

But 2 will also go into 6 and 8:

${ \text{ 6 $\div$ 2 } \over \text{ 8 $\div$ 2 } } { \text { = } } { \text { 3 } \over { 4 } }$

Clearly 4 is the 'highest common factor':

${ \text{ 12 $\div$ 4 } \over \text{ 16 $\div$ 4 } } { \text { = } } { \text { 3 } \over { 4 } }$

If you are unsure of what the highest common factor is, and if both the numerator and denominator are even – just start dividing by 2 and keep dividing by 2 until you get to an odd number.

For example, express 24/108 in its simplest form.

It can be difficult to see what the highest common factor is for both 24 and 108, but since the numbers are both even, start dividing by 2.

So, dividing by 2:

${ \text{ 24 $\div$ 2 } \over \text{ 108 $\div$ 2 } } { \text { = } } { \text { 12 } \over { 54 } }$

${ \text{ 12 $\div$ 2 } \over \text{ 54 $\div$ 2 } } { \text { = } } { \text { 6 } \over { 27 } }$

Now 27 is an odd number and we cannot keep dividing by 2 but we can see that 3 will both go into 6 and 27 to give:

${ \text{ 6 $\div$ 3 } \over \text{ 27 $\div$ 3 } } { \text { = } } { \text { 2 } \over { 9 } }$

So, 24/08 in its simplest form is 2/9.

If we now look at the process we used, we first divided by 2, divided by 2 again, then divided by 3 (which in effect is 2 times 2 times 3 = 12). Therefore the Highest Common Factor (HCF) of 24 and 108 is 12. If we were good at our times table we could have gone straight to 12.

For instance, it would look like:

${ \text{ 24 $\div$ 12 } \over \text{ 108 $\div$ 12 } } { \text { = } } { \text { 2 } \over { 9 } }$

So, to conclude, 24/108 is the same value as 2/9 (if you don’t believe it, plug the values into your calculator, they will both = 0.222222).

Operations with Fractions

In this section, we will look at performing mathematical calculations on fractions.

Multiplying Fractions

To multiply fractions you multiply the numerators and then multiply the denominators and simplify.

For example:

${ \text { Calculate } } { \text{ 2 } \over \text{ 5 } }$

Which looks like:

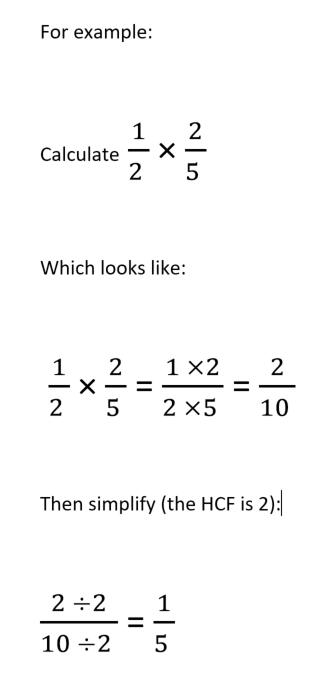
${ \text{ 12 $\div$ 2 } \over \text{ 16 $\div$ 2 } } { \text{ 12 $\div$ 2 } \over \text{ 16 $\div$ 2 } } { \text{ 12 $\div$ 2 } \over \text{ 16 $\div$ 2 } }$

To help you remember there is a rhyme!

Multiplying fractions not forgotten, top times top over bottom times bottom

- And don’t forget to simplify...

Dividing Fractions

To divide fractions, invert the second fraction (or what is known as taking the reciprocal) and then multiply.

To help you remember there is a rhyme!

Dividing fractions as easy as pie, flip the second fraction then multiply

- And don’t forget to simplify...

What is a reciprocal?

What's a Reciprocal | 2:06 mins

Addition and Subtraction of Fractions

To add or subtract fractions the denominators of the fractions must be the same.

Why?

Why do you need common denominators | 4:59 mins

Adding Fractions

Adding fractions uses the same process except you add the numerators. If instead of subtracting we added in the previous example, we would have:

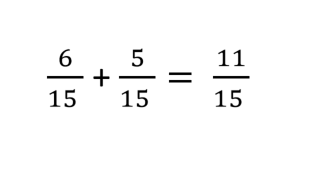
To help you remember there is a rhyme!

If adding or subtracting is your aim, the bottom numbers must be the same! Change the bottom using multiply, But the same to the top you must apply.

-And, don’t forget to simplify.

Final Thoughts

To recap: Remember that fractions are just like any other number. Remember the rules for doing calculations with fractions and it will become second nature.